Does adding gold to traditional stock bond portfolios provide diversification?
This question has been popping up on Twitter quite a bit recently. A notable example of this was the post by Bob Elliot shown in Figure 1.
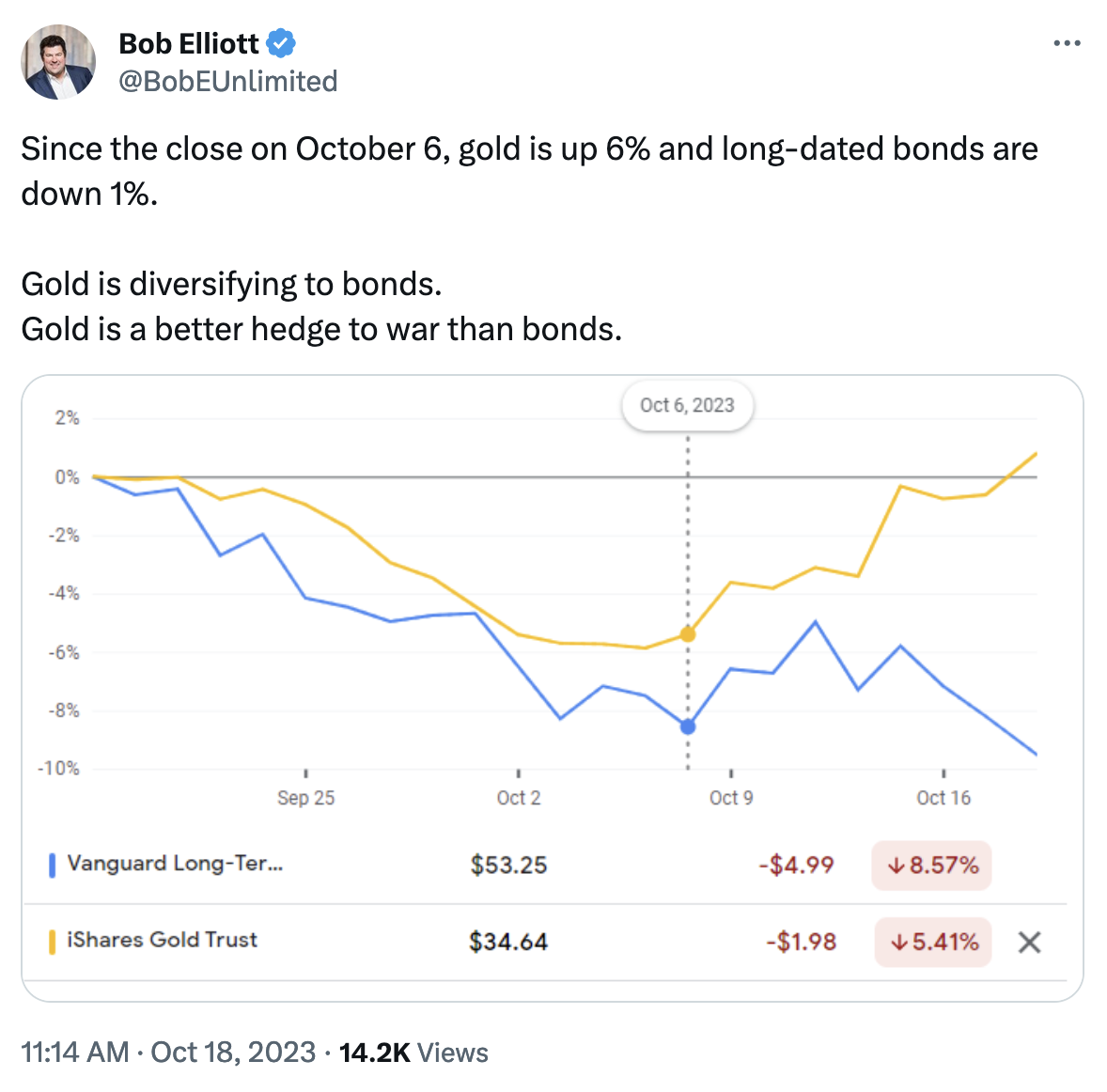
Figure 1: "Gold is diversifying to bonds."
We decided it would make for an interesting blog post to empirically test this assertion and write about it. The framework we will use 1,2 is a simple multivariate regression of the form shown in Equation 1.
$$ r_{gt} - r_f = \alpha_g + \beta_{m}\left(r_{mt} - r_f\right) + \beta_{b}\left(r_{bt} - r_f\right) + \epsilon_{gt} \qquad\qquad\qquad\qquad (1) $$ where $$r_{gt} := \text{gold return}$$ $$r_{mt} := \text{stock market return}$$ $$r_{bt} := \text{bond market return}$$ $$r_f := \text{risk free rate}$$ $$\alpha_g := \text{intercept}$$ $$\beta_{m} := \text{stock market exposure}$$ $$\beta_{b} := \text{bond market exposure}$$
The title of this post explains pretty plainly what questions we are attempting to answer. To be more specific, we will regress gold returns in excess of the risk free rate on excess stock and bond returns.
The securities we will use in the analysis to proxy each asset class are shown in Table 1.
| Ticker | Description | Asset Class |
|---|---|---|
| GLD | Russell 1000 | Gold |
| SPY | S&P 500 | Stocks |
| IEF | 7-10 Year Treasury | Bonds |
| TLT | 20 Year Treasury | Bonds |
| BIL | 1-3 Month T-Bill | Cash |
Table 1: ETF Proxies for Gold, Cash, Stocks, and Bonds
The reader will notice that we have chosen two ETFs to represent long-dated bonds. This was very intentional and, as we will see, the ETF we select to represent this asset class makes a huge differences. Ultimately, the answer to our original question is: It Depends!
Figure 1 shows the time-series of rolling parameters we estimate for Equation 1 where we define "long-dated" bonds using the 7-10 Year Treasury ETF (IEF).
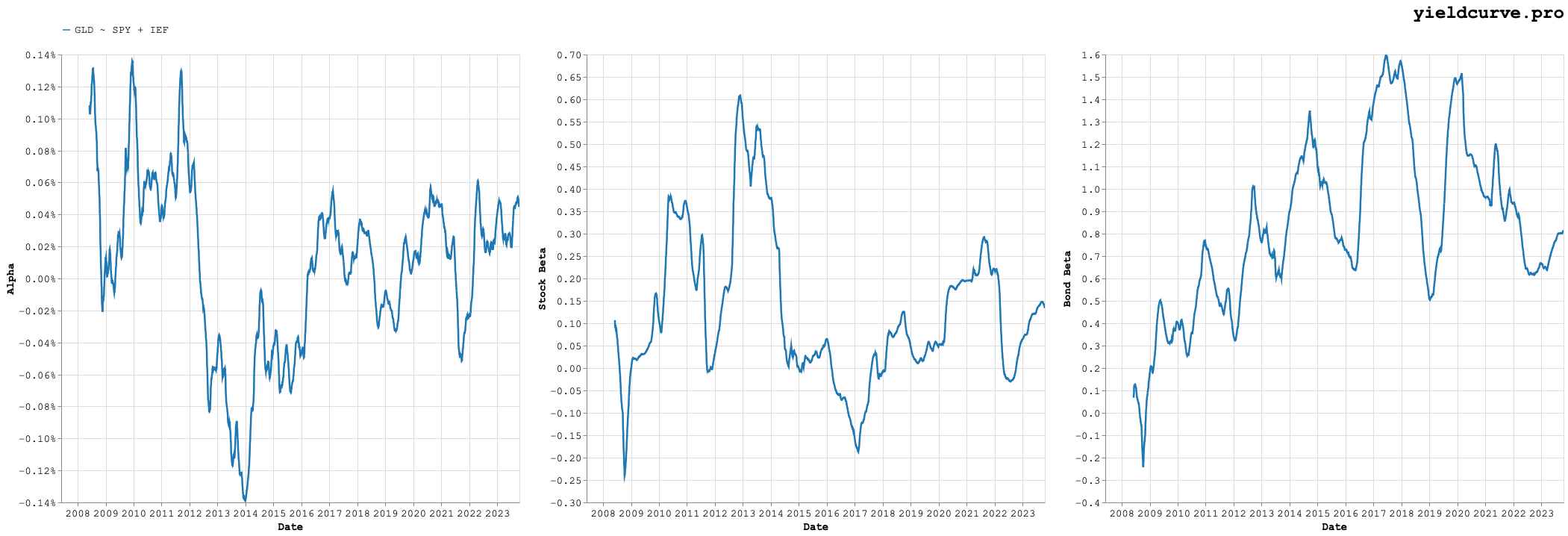
Figure 1: Rolling Alpha (Intercept), Stock, and Bond Beta (IEF Case)
Now we can split hairs regarding whether or not 7-10 years really constitute long. However, the result is interesting. We see that adding gold (or rather...GLD) results 189 basis points of alpha on an annualized basis. While this results in low exposure to stocks it does not lead to low exposure to bonds. This amounts, more or less, to a doubling down on bonds as expressed by IEF.
Swapping IEF for TLT says that we are now expressing our long-bond exposure by something truly long and we get the results shown in Figure 2.
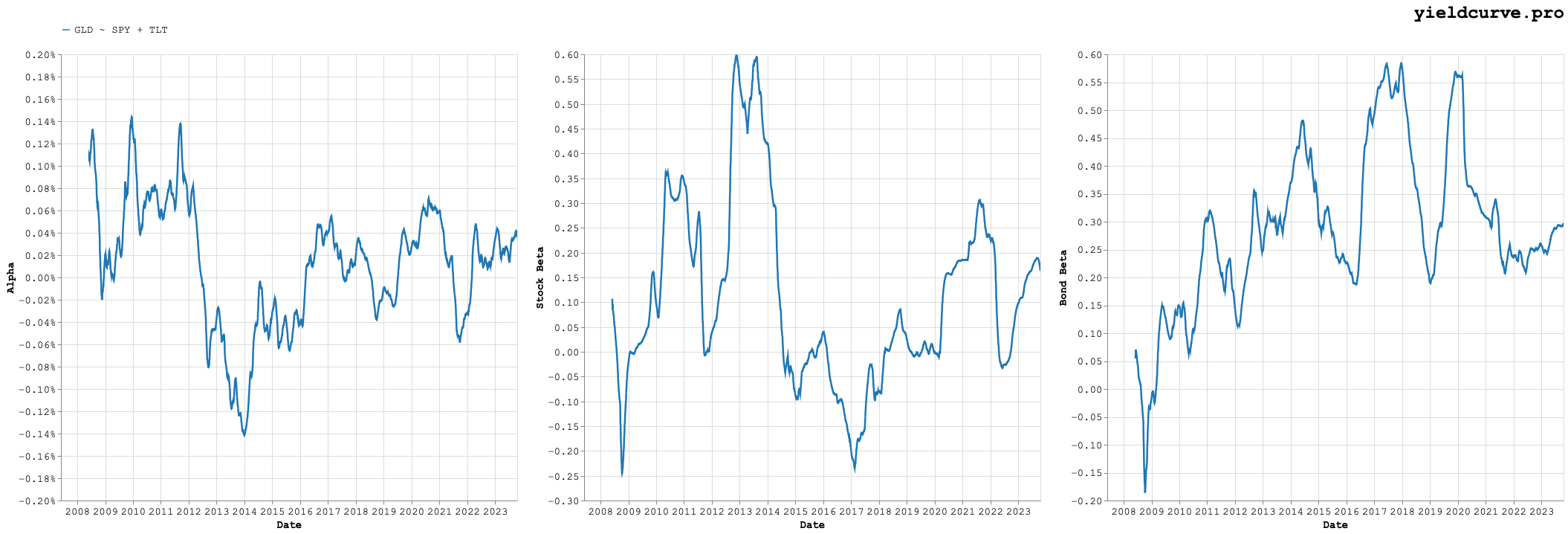
Figure 2: Rolling Alpha (Intercept), Stock, and Bond Beta (TLT Case)
TLT holds Treasury bonds with tenors in the 20 year range. This boosts alpha by roughly 100 basis points to sit around 283. This results in essentially the same stock exposure but with a significant reduction in bond beta. This is a diversifying addition and there do seem to be synergies adding gold in this case. Good call Bob!
Table 2 summarizes the average results over the time frame tested.
| Regression Variables | Alpha | Stock Beta | Bond Beta |
|---|---|---|---|
| GLD ~ SPY + IEF | 1.89 | 0.12 | 0.83 |
| GLD ~ SPY + TLT | 2.83 | 0.11 | 0.29 |
Table 2: Regressions and Their Average Estimated Parameters
In the end, adding gold to traditional stock bond portfolios does provide diversification. It just depends on which bonds we are talking about.
Back