Does adding gold to traditional stock-bond portfolios provide diversification (Part 2)?
In our last blog post we considered the following simple framework to determine the extent to which gold did or did not diversifying a classic portfolio of equities and Treasuries:
$$ r_{gt} - r_f = \alpha_g + \beta_{m}\left(r_{mt} - r_f\right) + \beta_{b}\left(r_{bt} - r_f\right) + \epsilon_{gt} \qquad\qquad\qquad\qquad (1) $$ where $$r_{gt} := \text{gold return}$$ $$r_{mt} := \text{stock market return}$$ $$r_{bt} := \text{bond market return}$$ $$r_f := \text{risk free rate}$$ $$\alpha_g := \text{intercept}$$ $$\beta_{m} := \text{stock market exposure}$$ $$\beta_{b} := \text{bond market exposure}$$
The determination of that simple study was that gold can add diversification depending on the tenor of the Treasuries added to the portfolio. To quantify the effect we begin with the same basic set of readily available ETFs as proxies for gold, cash, and stocks shown in Table 1.
| Ticker | Description | Asset Class |
|---|---|---|
| GLD | Russell 1000 | Gold |
| BIL | 1-3 Month T-Bill | Cash |
| SPY | S&P 500 | Stocks |
Table 1: ETF Proxies for Gold, Cash, and Stocks
To capture the different Treasury tenors we utilize the ETFs shown in Table 2.
| Ticker | Description | Asset Class |
|---|---|---|
| SHV | 1-12 Month Treasury | Bonds |
| SHY | 1-3 Year Treasury | Bonds |
| IEI | 3-7 Year Treasury | Bonds |
| IEF | 7-10 Year Treasury | Bonds |
| TLH | 10-20 Year Treasury | Bonds |
| TLT | 20+ Year Treasury | Bonds |
Table 2: ETF Proxies for Bonds
The resulting Bond and Stock exposures are shown in Figure 1.
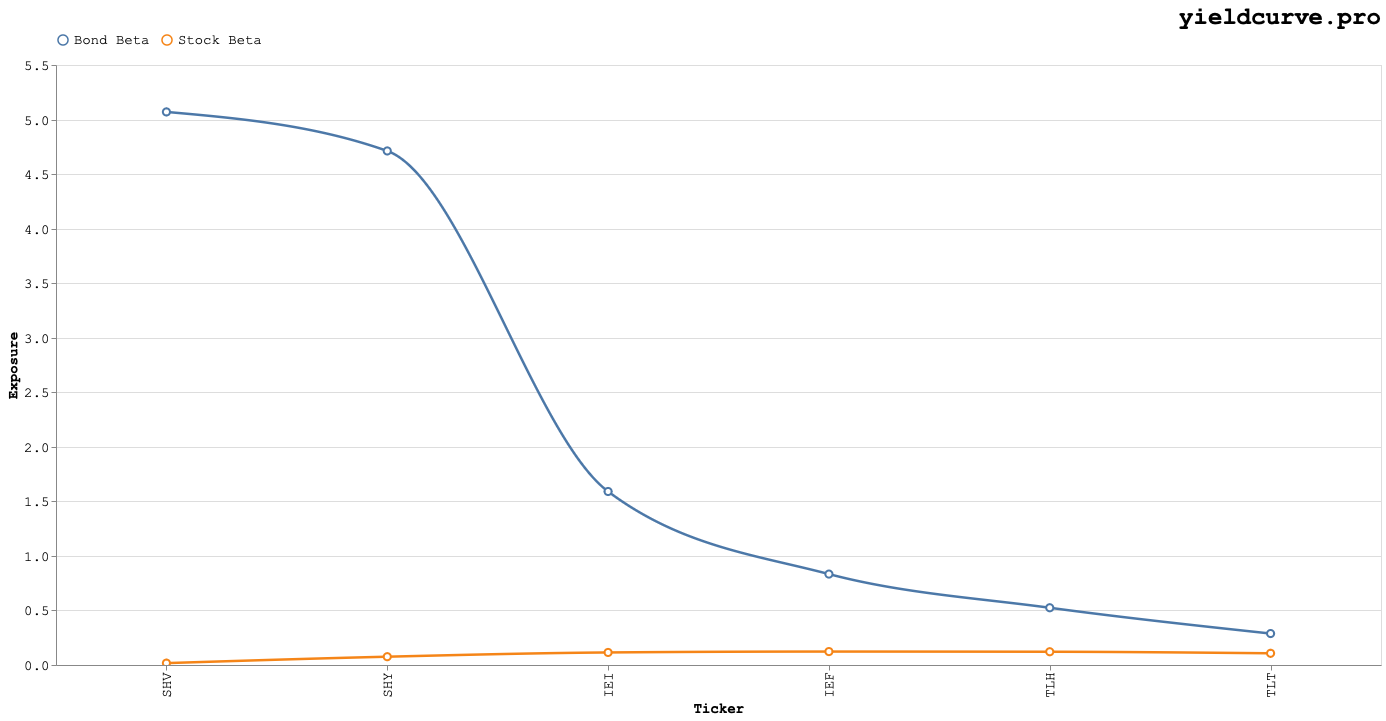
Figure 1: Gold Exposures to Bond ETFs Varying by Tenor
The Bond exposure is a monotonically decreasing function of tenor. Also, gold's Stock exposure is relatively muted compared to Bonds.
What does this simple analysis say? Essentially, it says that gold is a relatively good diversifier for a traditional stock-bond portfolio as long as the bonds are have tenors of about 20+ years.
Investors should be targeting TLH and TLT as the bond component of their portfolios if they plan to derive any diversification benefits from adding GLD.
Back